17 Oscillations (A2)

17.1 Simple Harmonic Oscillations

• Simple harmonic motion occurs when acceleration is proportional to the displacement from a fixed point and in the opposite direction. Terms such as displacement, amplitude, period, frequency, angular frequency, and phase difference are used to describe oscillations. The period can be expressed in terms of both frequency and angular frequency.

• The equation of motion for a simple harmonic oscillator is: a = -ω²x, where a is the acceleration, x is the displacement, and ω is the angular frequency. The solution to this equation is: x = x₀ sin(ωt), where x₀ is the amplitude of the oscillation.

• The velocity of an oscillator is given by: v = v₀ cos(ωt), where v₀ is the maximum velocity of the oscillator and the formula v = ± ω (sqrt(X₀² - X²) ).

• The kinetic and potential energy of an oscillator in simple harmonic motion interchange during the motion. The total energy of the oscillator is given by: E = 1/2mω² x₀², where m is the mass of the oscillator.

17.2 Damped and Forced Oscillations, Resonance

• Damping occurs when a resistive force acts on an oscillating system, causing it to lose energy over time.

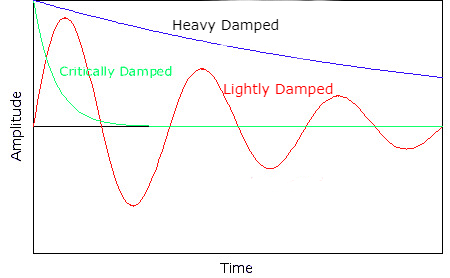
• Light, critical, and heavy damping are three types of damping. Light damping results in oscillations that slowly decay to zero, while heavy damping results in oscillations that do not oscillate at all. Critical damping results in the quickest return to equilibrium without overshooting.

• Resonance occurs when an oscillator is forced to oscillate at its natural frequency. At resonance, the amplitude of the oscillation is at a maximum. -- Types of Damping

17.3 Damping and Resonance

• Damping is the process of reducing the amplitude of an oscillation due to the presence of a resistive force. In an oscillating system, damping can be caused by friction, air resistance, or any other force that opposes the motion.

• The terms light, critical, and heavy damping refer to the amount of damping in an oscillating system. Light damping occurs when the resistive force is small, critical damping occurs when the resistive force is just enough to prevent oscillations from continuing indefinitely, and heavy damping occurs when the resistive force is large enough to cause the system to return to its equilibrium position without oscillating.

• Displacement-time graphs can be used to illustrate the different types of damping. Lightly damped systems will have a gradual decrease in amplitude over time, critical damping will result in the oscillations returning to equilibrium without any overshoot, and heavily damped systems will have a rapid decrease in amplitude and return to equilibrium without oscillating.

• Resonance occurs when an oscillating system is forced to oscillate at its natural frequency, resulting in a maximum amplitude of oscillations.